Question

On two investments totaling $6,000, Kevin lost 3% on one and earned 6% on the other. If his net annual receipts were $288, how much was each investment?

Answer 1

$ 800 was invested in the account at 3%

$5200 was invested in the account at 6%

Explanation:

We can establish the following system of equations thanks to the help of the statement:

Let x represent the amount invested in the investment that lost value

Let y represent the amount invested in the investment that gained

value.

`\begin{gathered} x+y=6000\rightarrow y=6000-x\text{ (1)} \\ -0.03x+0.06y=288\text{ (2)} \end{gathered}`

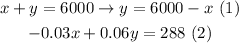
We replace equation (1) in (2) and solve for x:

`\begin{gathered} -0.03x+0.06\cdot(6000-x)=288 \\ -0.03x+360-0.06x=288 \\ -0.09x=288-360 \\ x=(-72)/(-0.09) \\ x=800 \\ \text{ Now, for y replacing in (1)} \\ y=6000-800=5200 \end{gathered}`

Therefore, $ 800 was invested in the account the lost value, and $ 5200 was invested in the account that gained value.