Question

What is the volume (in L) of 2.20 grams of CO2 gas at STP? (molar masses are, Carbon = 12.01 g/mol, and oxygen = 16.00 g/mol)

Answer 1

We will assume that we have an ideal gas, so we can apply the following equation:

`PV=nRT`
`V=(nRT)/(P)`

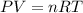
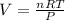
Where,

V is the volume of the gas in liters

n is the number of moles

R is a constant, 0.08206 atm.L/mol.K

T is the temperature of the gas, at STP conditions the temperature is 273.15K

P is the pressure of the gas, at STP conditions the pressure is 0.987atm.

We see that we have two unknowns, the number of moles and the volume.

The moles can be found by dividing the mass of the gas by its molar mass, the molar mass of CO2 is:

MolarMassCO2= 12.01g/mol + 16.00x2 g/mol=44.01g/mol

Now, we have that the moles of CO2 will be:

`molCO_2=givengCO_2*(1molCO_2)/(MolarMass,gCO_2)`
`molCO_2=2.20gCO_2*(1molCO_2)/(44.01gCO_2)=0.0500molCO_2`

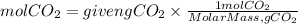
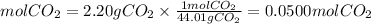
Therefore, the volume of the gas at STP conditions will be:

`\begin{gathered} V=(nRT)/(P) \\ V=(0.0500mol*0.08206(atm.L)/(mol.K)*273.15K)/(0.987atm)=1.13L \end{gathered}`

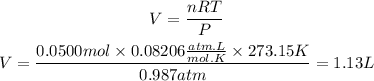
Answer: The volume of the gas will be 1.13L