Question

A bicycle travels 9.90 km due east in 0.500 h, then 9.00 km at 15.0° east of north in 0.770 h, and finally another 9.90 km due east in 0.500 h to reach its destination. The time lost in turning is negligible. Assume that east is in the +x-direction and north is in the +y-direction.What is the direction of the average velocity for the entire trip? Enter the answer as an angle in degrees north of eastWhat is the magnitude of the average velocity for the entire trip

Answer 1

First, draw a diagram to visualize the situation:

The average velocity v is defined as the quotient of the total displacement over the time that it takes to perform the displacement:

`\vec{v}=\frac{\Delta\vec{r}}{\Delta t}`

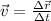
Notice that both velocity and displacement are vector quantities.

For that reason, the direction of the average velocity will be the same as the direion of the displacement.

Find the displacement by adding the three displacements as vectors. To do so, find the x and y components of each displacement, add the components to find the x and y components of the total displacement, and finally use the vertical and horizontal components of the total displacement to find the direction.

9.90 km East:

Since this vector points towards the East, its vertical component is 0.

The horizontal component is 9.90 km.

9.00 km 15.0º East of North

Since the angle of 15.0º is measured with respect to the positive Y axis, use the cosine function to find the vertical component and the sine function to find the horizontal component.

Vertical component:

Horizontal component:

9.90 km East:

Since this vector points towards the East, its vertical component is 0.

The horizontal component is 9.90 km.

Vertical component of the displacement:

Horizontal component of the displacement:

To find the direction in degrees north of east, notice that:

`\tan \theta=\frac{\text{Vertical component}}{\text{ Horizontal component}}`

Then:

The magnitude of a vector V with components V_x and V_y is:

`|V|=\sqrt[]{V^2_x+V^2_y}`

Then, the magnitude of the displacement is:

Divide the magnitude of the displacement by the total travel time to find the magnitude of the average velocity. The total time was 0.5h+0.77h+0.5h=1.77h.

Therefore, the answers are: