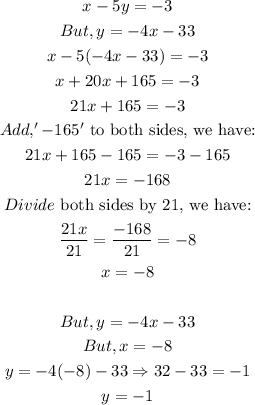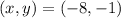Question

Solve the following system of equations with the substitution method:x — 5y = 3y = - 4x – 33{Answer: (x, y)

Answer 1

Let's begin by listing out the information given to us:

`\begin{gathered} x—5y=-3----1 \\ y=-4x-33---2 \end{gathered}`

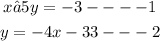
In substitution method, we make one of the unknown variables to be the subject of the formula. In this case, we already have equation 2 in this form:

`y=-4x-33`

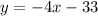
We then substitute that variable into the other equation (equation 1), so that the new equation is expressed in only one variable rather than two variables:

`\begin{gathered} x-5y=-3 \\ But,y=-4x-33 \\ x-5(-4x-33)=-3 \\ x+20x+165=-3 \\ 21x+165=-3 \\ Add,^(\prime)-165^(\prime)\text{ to both sides, we have:} \\ 21x+165-165=-3-165 \\ 21x=-168 \\ Divide\text{ both sides by 21, we have:} \\ (21x)/(21)=(-168)/(21)=-8 \\ x=-8 \\ \\ But,y=-4x-33 \\ But,x=-8 \\ y=-4(-8)-33\Rightarrow32-33=-1 \\ y=-1 \end{gathered}`
`(x,y)=(-8,-1)`