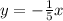ANSWER
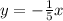
Step-by-step explanation
As we can see, line j passes through the origin, so its y-intercept is zero and the equation has the form,
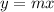
To find the slope we have to use the formula,
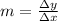
In this graph,
Δy = 1 and Δx = 5, but the line is inclined to the left, so the slope is negative,
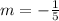
And the equation is,