In sine and cosine functions, we have the following forms:
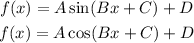
Where A is the amplitute, 2π/B is the period, C is the phase shift and D is the vertical shift.
By comparison, we can see that:
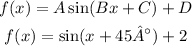
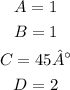
Then, the phase shift is 45°, the vertical shift is 2.
The vertical shift is the same as the middle horizontal axis of the function, so we know that the middle of the function is y = 2. The amplitute is how many units the function varies up and down from the middle. Since the Amplitute is 1, the function varies from 2 - 1 to 2 + 1, that is, it varies from 1 to 3. So, the range of the function is:
![R=\left[1,3\right]](https://img.qammunity.org/2023/formulas/mathematics/college/ob3fuf5i648g1b8jo97i6qvgaieu6yqxf1.png)