Question

write your answer for each part. make sure to label each part: , , and Children and Adults purchased tickets for a local amusement park. All tickets were sold at the park entrance - season passes, discounts, etc. we're not allowed. A childs ticket cost $8 while an adult ticket cost $15. A total of $5,500 was collected. 600 tickets were sold. : Write a system of equations that can be used to find the number of children's tickets, c, and the number of adult tickets, a, that were sold at the amusement park : How many of each type of ticket were sold? Must show evidence to support your answer. state your answer using a complete sentence. : Assuming that the number of children and adults visiting the park would not change, how much more money could you have been collected if the park charged children and adults the same price of $15? make sure to answer a complete sentence. Show evidence to support your answer

Answer 1

Part A

We are asked to write a system of equations to calculate the amount of tickets sold of each type (choldren and adults). We are told that 600 tickets were sold. Let's say the number of children's tickets is c, and the number of adult tickets is a. Then:

`c+a=600`

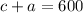
The total amount of money collected was $5500. The tickets for children cost $8, and $15 for adults. Then:

`8c+15a=5500`

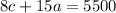
Now, we can create a system of two equations with two unknowns: c and a.

`\begin{gathered} c+a=600 \\ 8c+15a=5500 \end{gathered}`

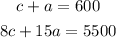
This system of equations will allow us to caluclate how many children tickets and how many adult tickets were sold.

Part B

We need to calculate how many of each type were sold. We have the system of equations that will allow us to do that. To use substitution method from the first equation we can solve for c:

`c=600-a`

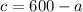
Now that we have an expression for c, we can replace it in the second equation of the system:

`8(600-a)+15a=5500`

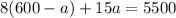
In the previous expression, we have now only one unknown: a. Then, we can easily solve it:

`4800-8a+15a=5500`

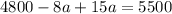
Reducing like terms (-8a and 15a):

`\begin{gathered} 4800+7a=5500 \\ 7a=5500-4800 \\ 7a=700 \\ a=(700)/(7) \\ a=100 \end{gathered}`

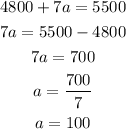
Now we have calculated the amount of adult tickets sold: 100. Now, knowing this value, we can recall the first equation of the system (c + a = 600) and estimate the number of children's tickets sold:

`\begin{gathered} c+a=600 \\ c+100=600 \\ c=600-100 \\ c=500 \end{gathered}`

Now, we also know the number of children's tickets sold: 500.

We can prove this recalling the system of equations. The total number of tickets sold was 600. 500 for children plus 100 for adults give as the 600 tickets sold:

`\begin{gathered} c+a=600 \\ 500+100=600 \\ 600=600 \end{gathered}`

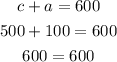
Also, calculating the total amount of money collected:

`\begin{gathered} 8c+15a \\ 8\cdot500+15\cdot100 \\ 4000+1500=5500 \end{gathered}`

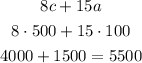
We obtain $5500, the same amount stated at the beggining of the problem. Now, those amounts are confirmed: 500 shildren tickets were sold, while for adults, only 1000 were sold.

Part C

Now, we are told to estimate how much more money would have been earned if the same amount of children and adult tickets were sold, but the children tickets costing $15.

The number of children and adults is kept the same: c = 500 and a = 100.

We can calulate the new hypothetical earnings:

`\begin{gathered} 15\cdot c+15\cdot a \\ 15\cdot500+15\cdot100 \\ 7500+1500=9000 \end{gathered}`

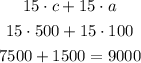
With the new ticket fees, the total earning would have been $9000. Recalling that the earning with old fees were $5500, then:

`9000-5500=3500`

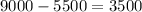
Then, with the new fees, they wuold earn $3500 more than with the old fees.