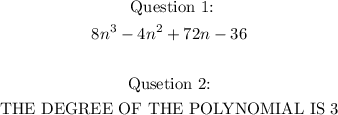Question

Simplify by finding the product of the polynomials below. Then Identify the degree of your answer. When typing your answer use the carrot key ^ (press shift and 6) to indicate an exponent. Type your terms in descending order and do not put any spaces between your characters. (8n-4)(n^2+9) This simplifies to: AnswerThe degree of our simplified answer is: Answer

Answer 1

`\begin{gathered} \text{ Question 1:} \\ 8n^3-4n^2+72n-36 \\ \\ \text{Qusetion 2:} \\ \text{THE DEGREE OF THE POLYNOMIAL IS 3} \end{gathered}`

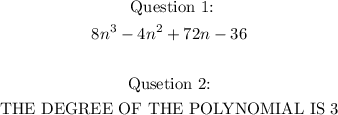
SOLUTION

Problem Statement

The question gives us an expression to simplify and we are to simplify by finding the product. We are also asked to find the degree of the polynomial as well

Method

We simply need to expand the bracket to solve this question. But the degree of the polynomial is gotten by assessing which term in the final expression has the highest power. If the expression has a term with its highest power being 3, then the degree of the polynomial is 3.

With this information, let us begin solving.

Implementation

1. Expanding the expression:

Expanding the polynomial, we have:

`\begin{gathered} (8n-4)(n^2+9) \\ \text{ Using the FOIL method,} \\ F=8n(n^2)=8n^3 \\ O=8n(9)=72n \\ I=-4(n^2)=-4n^2 \\ L=-4(9)=-36 \\ \\ \therefore(8n-4)(n^2+9)=8n^2+72n-4n^2-36 \\ \\ \text{ Remember, we are asked to write this result in descending order of terms. Thus, we have that:} \\ 8n^3-4n^2+72n-36 \end{gathered}`

2. Degree of the polynomial:

From the above result, we can see that the highest degree of n in all the terms is 3, therefore, the degree of the polynomial is 3

Final answer

`\begin{gathered} \text{ Question 1:} \\ 8n^3-4n^2+72n-36 \\ \\ \text{Qusetion 2:} \\ \text{THE DEGREE OF THE POLYNOMIAL IS 3} \end{gathered}`