Considering the right triangle ABC
Side a is opposite to ∠A and adjacent to ∠B
Side b is opposite to ∠B and adjacent to ∠A
To determine the length of "a" given that we know the length of b and the measure of ∠B, you have to apply the trigonometric ratio of the tangent which is defined as follows:

The tangent of an angle "θ" is equal to the quotient between the opposite side of the angle and the adjacent side.
As mentioned before, considering ∠B, side b is opposite to this angle, and side a is adjacent to it.
Replace ∠B=70º and b=16 into the expression of the tangent:
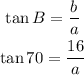
Multiply both sides by "a" to take the term from the denominator's place:
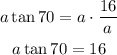
Divide both sides by the tangent of 70 to determine the length of a:
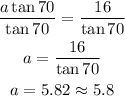
Side a is 5.8 units long. (first option)