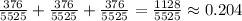Question

Three cards are dealt without replacement what is the probability that exactly one is an ace? please explain

Answer 1

Answer: 1128/5525 = 0.204

There are 52 cards in one deck. First, we list down all the probabilities of picking exactly one ace for each deal:

Getting an ace as the first card:

`\begin{gathered} P(A)=(4)/(52) \\ P(C|A)=(48)/(51) \\ P(C|CA)=(47)/(50) \\ P(ACC)=(376)/(5525)\approx0.068 \end{gathered}`

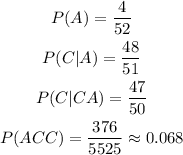
Then, we will find the probability of getting an ace as the second card:

`\begin{gathered} P(C)=(48)/(52) \\ P(A|C)=(4)/(51) \\ P(C|AC)=(47)/(50) \\ P(CAC)=(376)/(5525)\approx0.068 \end{gathered}`

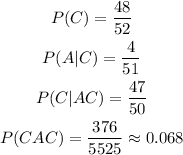
Then, the probability of getting an ace on the third card:

`\begin{gathered} P(C)=(48)/(52) \\ P(C|C)=(47)/(51) \\ P(A|CC)=(4)/(50) \\ P(CCA)=(376)/(5525)\approx0.068 \end{gathered}`

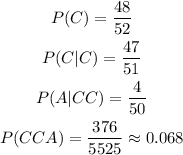
We will then add all of these probabilities:

`(376)/(5525)+(376)/(5525)+(376)/(5525)=(1128)/(5525)\approx0.204`