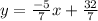The point-slope equation is the following:
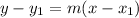
Where (x1, y1) is a point of the line and m is the slope.
The slope is calculated as:
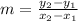
Where (x1, y1) and (x2, y2) are points of the line. So, replacing (x1, y1) by (-2, 6) and (x2, y2) by (5, 1), we get:
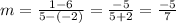
Then, the point-slope form is:
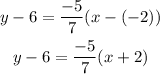
Finally, to rewrite the equation in slope-intercept form, we need to solve for y as:
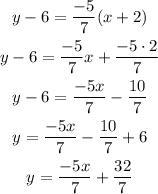
Answer: Point-slope form:
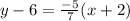
Slope-Intercept form: