1 Answer

Chandrika Joshi · Answer 1 · 2023-06-19T05:55:58+0000

We are given the following system of equations:

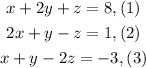
$\begin{gathered} x+2y+z=8,(1) \\ 2x+y-z=1,(2) \\ x+y-2z=-3,(3) \end{gathered}$

To solve the system we will add equations (1) and (2):

Adding like terms:

$\begin{gathered} 3x+3y=9 \\ x+y=3,(4) \end{gathered}$

Now we multiply equation (2) by -2:

Now we add this equation to equation (3):

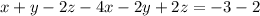
Adding like terms:

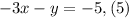
Now we add equations (4) and (5):

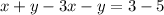
Adding like terms:

Dividing both sides by -2:

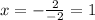
Now we replace this value of "x" in equation (4):

$\begin{gathered} x+y=3 \\ 1+y=3 \end{gathered}$

Subtracting 1 to both sides:

$\begin{gathered} 1-1+y=3-1 \\ y=2 \end{gathered}$

Now we replace the values of "x" and "y" in equation (1):

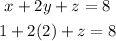
$\begin{gathered} x+2y+z=8 \\ 1+2(2)+z=8 \end{gathered}$

Adding like terms:

$\begin{gathered} 1+4+z=8 \\ 5+z=8 \end{gathered}$

Subtracting 5 to both sides:

$\begin{gathered} 5-5+z=8-5 \\ z=3 \end{gathered}$

Therefore, the solution of the system is:

$x=1,\text{ y=2, z=3}$

Please log in or register to add a comment.