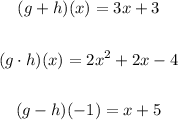Given:
g(x) = x - 1
h(x) = 2x + 4
Let's evaluate the functions for (g+h)(x) and (g.h)(x)
• (g+h)(x):
Here all we have to do is to add up both functions.
We have:
(g + h)(x) = g(x) + h(x)
= (x - 1) + (2x + 4)
= x - 1 + 2x + 4
= x + 2x + 4 - 1
= 3x + 3
Thus,
(g + h)(x) = 3x + 3
• (g.h)(x)
This is to multiply both functions.
We have:
(g.h)(x) = g(x) * h(x)
= (x - 1)(2x + 4)
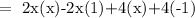
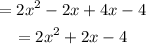
• Evaluate (g - h)(-1):
First evaluate (g - h)(-1)
Use distributive property to distribute the -1 into g and h.
(g(-1) -h(-1))
= -g + h
Now evaluate (-g + h):
(-g + h) = -(x -1) + (2x + 4)
= -x + 1 + 2x + 4
= -x + 2x + 1 + 4
= x + 5
ANSWER: