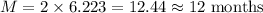Question

Within two months of birth, a pair of the fish known as guppies can produce 50 offspring in the first generation. If half of those are females, each of the 25 females can produce 50 offspring. There would be 25 · 50 = 1250 guppies in the second generation, 25 · 1250 = 31,250 guppies in the third generation, and 781,250 guppies in the fourth generation. Assume this pattern continues; ignore additional births, predators, sickness, etc. Assume that 1 generation = 2 months.------In how many months would there be over 10^10 (ten billion) guppies? Group of answer choices20 months12 months24 months14 months

Answer 1

- The formula for the reproduction can be derived as follows:

`\begin{gathered} f(1)=50(25)^0 \\ f(2)=50(25)=1250 \\ f(3)=50(25)^2=50(25)^2=31250 \\ \text{ And so on...} \\ \text{ We can generalize for the nth generation as} \\ \\ f(n)=50(25)^(n-1) \\ \\ where, \\ n=\text{ Number of 2month periods} \\ f(n)=\text{ Number of guppies} \end{gathered}`

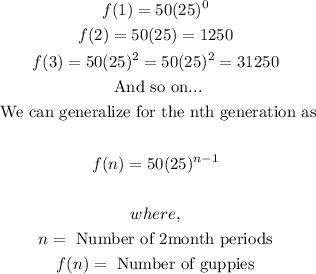
- With the general formula, we can proceed to solve the question.

- This is done below:

`\begin{gathered} f(n)=10^(10) \\ \\ f(n)=50(25)^(n-1)=10^(10) \\ (100)/(2)(25)^(n-1)=10^(10) \\ \\ \text{ Divide both sides by 100. Multiply both sides by 2} \\ 25^(n-1)=2*(10^(10))*(1)/(100) \\ \\ 25^(n-1)=2*10^(10)*10^(-2)=2*10^8 \\ \\ (25^n)/(25)=2*10^8 \\ \\ 25^n=25(2*10^8) \\ \text{ Take the natural log of both sides} \\ \\ \ln25^n=\ln(50*10^8)=\ln((10^9)/(2)) \\ \\ n\ln25=\ln((10^9)/(2)) \\ \\ \text{ divide both sides by }\ln25 \\ \\ n=(\ln((10^9)/(2)))/(\ln25) \\ \\ n\approx6.223 \end{gathered}`

- Thus, there are 6.223 2-month periods for the guppies to have 10 billion babies.

- Therefore, the number of months is

`M=2*6.223=12.44\approx12\text{ months}`