Question

a person is watching a boat from the top of a lighthouse the boat is approaching the lighthouse directly. when first knows the angle of the depression to the boat is 16° 18' when the boat stops the angle of the depression is 48° 51' the lighthouse is 200 ft tall how far did the boat travel from when it was first noticed until it stopped? (round your answer to the nearest hundredth place and label appropriate units)

Answer 1

509.17 ft

Step-by-step explanation:

We can use the following model to represent the situation when the boat was first noticed.

So, we need to calculate the angle A and the distance x. For angle A, we get:

A = 90° - 16° 18' = 73° 42' =73.7

Now, using the trigonometric function tangent, we can calculate the value of x as follows:

`\begin{gathered} \tan 73.7=(x)/(200) \\ 200*\tan 73.7=x \\ 683.95\text{ ft = }x \end{gathered}`

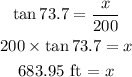
In the same way, we model the situation when the boat stops as follows:

Therefore, the value of angle B and the distance y are equal to:

B = 90° - 48° 51' = 41° 9' = 41.15°

`\begin{gathered} \tan \text{ 41.15 =}(y)/(200) \\ 200*\tan 41.15=y \\ 174.78\text{ ft = y} \end{gathered}`

Finally, the distance that the boat travel from when it was first noticed until it stopped can be calculated as the distance x less the distance y. So:

x - y = 683.95 ft - 174.78 ft = 509.17 ft

Therefore, the answer is 509.17 ft