Question

Write each function in vertex form, and identify its vertex. F(x)=x^2–10x+19

Answer 1

The vertex of a parabolla can be found by using the following expression:

`x=(-b)/(2a)`

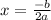
For this parabolla we have:

`x=(-(-10))/(2\cdot1)=(10)/(2)=5`

To find the y-coordinate we can apply the value of x for the vertex and evaluate the expression:

`F(x)=(5)^2-10\cdot5+19=-6`

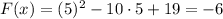
The vertex is on the coordinates (5,-6).

The vertex form of a parabola is given by:

`f(x)=d\cdot(x-h)^2+k`

Where (h,k) are the coordinates of the vertex for the parabolla. For this parabolla we have:

`f(x)=d\cdot(x-5)^2-6`

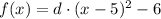
To find the value of d we can use the standard expression for the parabolla, as shown below:

`\begin{gathered} f(x)=d\cdot(x^2-10x+25)-6 \\ f(x)=d\cdot x^2-10\cdot d\cdot x+25\cdot d-6 \end{gathered}`

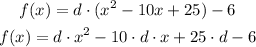
The value of d must make the expression above equal to the original parabolla. Therefore d must be 1.

`f(x)=(x-5)^2-6`