We have a right triangle from which we know the length of its hypotenuse (the side opposite to the right angle, 28 in this case), and the length of one hick, 20 (hicks are the sides forming the right angle). To find the length of the third side we can use the Pythagorean theorem, an equation that relates the 3 sides of a right triangle:

Where c is the hypotenuse, and a and b are the two hicks. We can replace values:
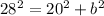
And now we can solve for the unknown side:
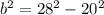
![b=\sqrt[]{784-400}](https://img.qammunity.org/2023/formulas/mathematics/college/q97cr3q4nxbdqjwfgx1jglyxfw12ptek39.png)
![b=\sqrt[]{384}](https://img.qammunity.org/2023/formulas/mathematics/college/219yx3cwcc02jua3d6vfvli2dwcup0r4nz.png)
Now, we can represent 384 as the product of smaller numbers by decomposing it:
384 | 2
192 | 2
96 | 2
48 | 2
24 | 2
12 | 2
6 | 2
3 | 3
1
Then, 384 can be written as 364 = 2*2*2*2*2*2*2*3:
![b=\sqrt[]{384}=\sqrt[]{2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot3}](https://img.qammunity.org/2023/formulas/mathematics/college/zoxpzievb6vycl2vbooy4qge88dt5kwspn.png)
![b=\sqrt[]{2^2\cdot2^2\cdot2^2\cdot2\cdot3}](https://img.qammunity.org/2023/formulas/mathematics/college/vtk82uxflssjbrkz65rhsjdekeojycv5nf.png)
Recalling that the square root of a product is equal to the product of the square roots:
![b=\sqrt[]{2^2}\cdot\sqrt[]{2^2}\cdot\sqrt[]{2^2}\cdot\sqrt[]{2\cdot3}](https://img.qammunity.org/2023/formulas/mathematics/college/s40zmqr3z2m5fmugudib94rq3v22222l7o.png)
![\begin{gathered} b=2\cdot2\cdot2\cdot\sqrt[]{6} \\ b=8\cdot\sqrt[]{6} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rub5t5g8ftnr7bfy0grbq09fdin6klt2rz.png)
Now we have the simplified value of the third side.
Solving and rounding:
