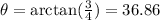Question

Draw the triangle and find the reference angle and then find the indicated trig function. How do i solve this problem?

Answer 1

Given:

`\csc (\theta)=(5)/(3)\text{ and }\cos (\theta)<0`

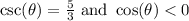
We want to find the value of tan(θ).

First, remember that cos(θ) is negative in the quadrants II and III of the xy-plane. Notice that as cscθ is positive (5/3), our reference angle should be located at the quadrant II.

We have to also remember that csc(θ) is a function that relations the hypotenuse of a right triangle and the opposite side to θ.

So, we could draw this situation here below:

Now, remember that tan(θ) is defined as the ratio between the opposite side to θ and its adjacent side.

So, we might need to find the adjacent side to θ in the triangle given. For this, we could use the Pythagorean theorem as follows:

As you can see, the adjacent side (a), is 4.

Then,

`\tan \theta=(3)/(4)`

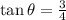
And, the value of θ will be:

`\theta=\arctan ((3)/(4))=36.86`