Question

Question 10 (Essay Worth 10 points)(04.05, 04.06 MC)Michael has $15 and wants to buy a combination of school lunches to feed at least three classmates. A sandwich costs $2, and hot lunch costs $3.This system of inequalities models the scenario:2x + 3y ≤ 15x + y ≥ 3Part A: Describe the graph of the system of inequalities, including shading and the types of lines graphed. Provide a description of the solution set. (4 points)Part B: Is the point (5, 1) included in the solution area for the system? Justify your answer mathematically. (3 points)Part C: Choose a point in the solution set and interpret what it means in terms of the real-world context. (3 points)

Answer 1

Part A: You have the followinf system of inequalities:

`\begin{gathered} 2x+3y\le15 \\ x+y\ge3 \end{gathered}`

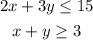
In order to determine the solution of the previous system, solve the previous inequalities for y:

`\begin{gathered} y\leq-(2)/(3)x+(15)/(3)\Rightarrow y\leq-(2)/(3)x+5 \\ y\ge-x+3 \end{gathered}`

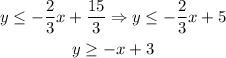
Now, take the previous inequalities as equations and graph the lines with a solid line (it means that values on the line are included in the solution for each inequality, due to the symbol of the inequality is ≤ and ≥):

The solid red line is the line for the first inequality. Due to in this inequality you have the symbol ≤, the valid solutions are all values below the line. The red shaded region has all solutions for this inequality.

The blue solid line represents the second inequality. Again, due to this inequality has the symbol ≥, it means that the valid solutions are all values above the line. The blue shaded region represent allsolutions of the second inequality.

The solution to the system is given by the region at which the red region and blue region overlap between them. As you can notice, the regions start to overlap at point (-6,9).

Part B: The point (5,1) is in the region of the overlapping of the blue and red region. It means that point (5,1) is a solution of the system.

Part C: you can select any point of the solution region. For instance, the point (3,1). This solution means that with the money Michael has, He is able to buy 3 sandwichs and 1 hot lunch.