Because we don’t have the initial value, we substitute both points into an equation of the form
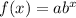
and then solve the system for a and b.
- Substituting (-3,4) gives:
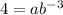
- Substituting (2,3) gives:
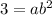
Use the first equation to solve for a in terms of b:

Substitute a in the second equation, and solve for b:
![\begin{gathered} 3=ab^2 \\ 3=4b^3b^2 \\ 3=4b^(3+2) \\ 3=4b^5 \\ (3)/(4)=b^5 \\ b=\sqrt[5]{(3)/(4)}=((3)/(4))^{(1)/(5)}=0.944 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vsqcnyeo3h76ts9jhejuyi0hpfi9k6q85d.png)
Use the value of b in the first equation to solve for the value of a:
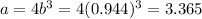
Thus, the equation is:
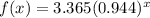
Next, we can graph the function:
Notice that the graph below passes through the initial points given in the problem (-3,4) and (2,3). So, the graph is an exponential decay function.
Answer:
- Equation
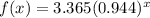
- This is an exponential decay function.