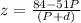Question

Solve for z.Remember: you are solving for an unknown coefficient, not the value of the variable as a number.-P(51 + z) = dz +84

Answer 1

- P ( 51 + z ) = dz + 84

First we divide both sides of the equation by -P.

`\begin{gathered} (-P(51+z))/(-P)=(dz)/(-P)+(84)/(-P) \\ 51+z=(dz)/(-P)+(84)/(-P) \\ 51+z=-(dz)/(P)-(84)/(P) \end{gathered}`

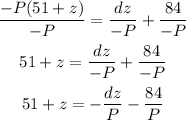
Now, we transpose all the terms with the variable z on the left side of the equation, and the constants on the right., and

`\begin{gathered} 51+z=-(dz)/(P)-(84)/(P) \\ z+(dz)/(P)=-(84)/(P)-51 \end{gathered}`

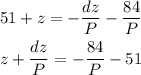
Then we'll add the terms on the left and on the right side of the equation.

`\begin{gathered} z+(dz)/(P)=-(84)/(P)-51 \\ (zP+dz)/(P)=(-84-51P)/(P) \\ \end{gathered}`

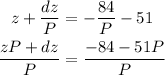
We can cross out the denominator P, since it appears on both sides of the equation. The resulting equation is:

`\begin{gathered} zP+dz=84-51P \\ \end{gathered}`

We have to factor out z on the left, so we can come up with an expression for z

`z(P+d)=84-51P`

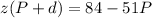
Then we divide both sides of the equation by ( P + d )

`\begin{gathered} z(P+d)=84-51P \\ (z(P+d))/((P+d))=(84-51P)/((P+d)) \\ z=(84-51P)/((P+d)) \end{gathered}`

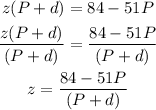
Answer:

`z=(84-51P)/((P+d))`