Recall the Law of Cosines:
If a triangle has sides with lengths A, B and C and the angle opposite to C has a measure θ, then:
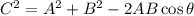
Since the side AE is opposed to the angle ABE in the triangle ABE, then:
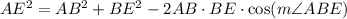
Find the values of AB and the measure of the angle ABE, and substitute those values along with the measure of BE into this equation to find AE.
First, notice that the triangle ABC is a right triangle, whose hypotenuse is AB.
The angle ABC is given and has a measure of 31°. Then:
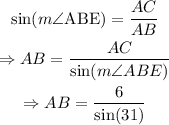
On the other hand, the angles ABC, ABE and EBD form an angle of 180°. Use this fact to find the measure of ABE:
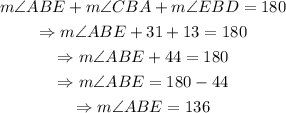
Substitute AB=6/sin(31), mABE=136° and BE=7 into the equation for AE:
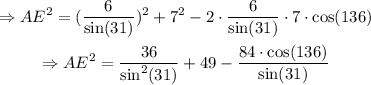
Use a calculator to find the value of AE^2:
![\begin{gathered} \Rightarrow AE^2=302.0342\ldots \\ \Rightarrow AE=\sqrt[]{302.0342\ldots} \\ \Rightarrow AE=17.379\ldots \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/cbj98ihny1zs8vcb9yzisn78p4drbh9ike.png)