Question

On this problem, the answer has been worked out, but you must fill in the blanks in the solution.A random sample of 450 students from a wide geographical area indicated that 55 attended private schools. Estimate the true proportion of students attending private schools with 95% confidence. Give your answer to three places after the decimal point.Solution: We need to find the 95% confidence interval for the proportion (p).

Answer 1

State the parameters given in the question

`n=450`

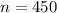
The sample size n is 450

Hence, the first box n=450

`X=55`

The number of students X that attended private school is 55

Hence, the second box X=55

Therefore, sample proportion is

`\begin{gathered} ^(\prime)p=(X)/(n)=(55)/(450) \\ ^(\prime)p=0.122 \end{gathered}`

Hence, the third box is 'p=0.122

`\begin{gathered} ^(\prime)q=1-^(\prime)p \\ ^(\prime)q=1-0.122 \\ ^(\prime)q=0.878 \end{gathered}`

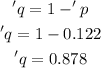
Hence, the forth box is 'q= 0.878

From the question, the confidence interval is 95% can be represented as

`\begin{gathered} z_(\alpha I2)=95\text{ \%=0.95} \\ \alpha=1-0.95=0.05 \\ \alpha I2=(0.05)/(2)=0.025 \end{gathered}`

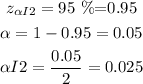
The Z score for confidence interval of 95% is gotten from the table as 1.96

The formula for the confidence interval for p is

`^(\prime)p-z_(\alpha I2)\sqrt[]{(^(\prime)p^(\prime)q)/(n)}<p>Substitute into the formula</p>[tex]\begin{gathered} ^(\prime)p-z_(\alpha I2)z_(\alpha I2)\sqrt[]{(^(\prime)p^(\prime)q)/(n)} \\ ^(\prime)p=0.122;^(\prime)q=0.878;z_(\alpha I2)=1.96 \\ =0.122-1.96_{}\sqrt[]{(0.122*0.878)/(450)} \\ =0.122-1.96\sqrt[]{(0.107116)/(450)} \\ =0.122-1.96\sqrt[]{0.0002380356} \\ =0.122-1.966(0.015428) \\ =0.122-0.03024 \\ =0.09176 \\ =0.092(3\text{ decimal places)} \end{gathered}`
`\begin{gathered} z_(\alpha I2)\sqrt[]{(^(\prime)p^(\prime)q)/(n)}\text{was calculated to be 0.03024} \\ \text{Therefore} \\ ^(\prime)p+z_(\alpha I2)\sqrt[]{(^(\prime)p^(\prime)q)/(n)}=0.122+0.03024=0.15224 \\ =0.152(3\text{decimal places)} \end{gathered}`

Hence, the confidence interval is 0.092