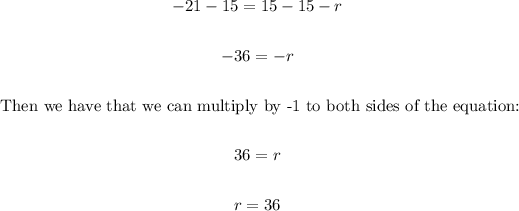Question

The points (6,r) and (−22, 15 ) on a line with slope −3/4. Find the missing coordinate r.

Answer 1

We have the following two points that belong to a line:

`(6,r)\text{ and }(-22,15)`

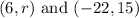
And also the slope of the line:

`m=-(3)/(4)`

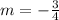
And we have to find the missing coordinate r.

To find that, we can proceed as follows:

1. We can label both points as follows:

• (6, r) ---> x1 = 6, y1 = r

,

• (-22, 15) ---> x2 = -22, y2 = 15

2. Now, we can use the formula for the slope of a line - since the slope of the line was given. Then we have:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \\ m=-(3)/(4) \end{gathered}`

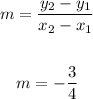
3. Then we can substitute the corresponding values into the above equation as follows:

`\begin{gathered} m=(y_(2)-y_(1))/(x_(2)-x_(1)),m=-(3)/(4),x_1=6,y_1=r,x_2=-22,y_2=15 \\ \\ -(3)/(4)=(15-r)/(-22-6) \end{gathered}`

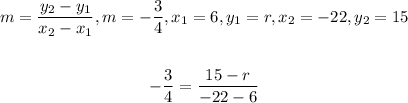
4. And now, we have to solve the equation for r as follows:

`\begin{gathered} -(3)/(4)=(15-r)/(-28) \\ \\ \text{ Multiply by -28 to both sides of the equation:} \\ \\ -28(-(3)/(4))=(-28\left(15-r\right))/(-28) \\ \\ (-28)/(4)(-3)=(28)/(28)(15-r) \\ \\ -7(-3)=15-r \\ \\ 21=15-r \end{gathered}`

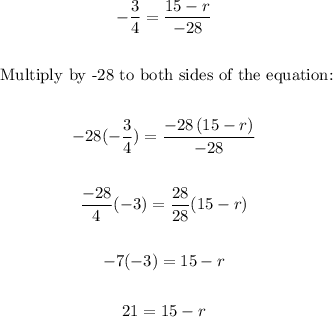
5. Finally, we can subtract 15 from both sides of the equation:

`\begin{gathered} -21-15=15-15-r \\ \\ -36=-r \\ \\ \text{ Then we have that \lparen we can multiply by -1 to both sides of the equation\rparen:} \\ \\ 36=r \\ \\ r=36 \end{gathered}`