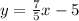We know that parallel lines have the same slope, this means that the searched line has the form
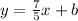
This is because the slope is the coefficient of x on the given line equation:
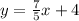
Now, we can find by y-intercept, denoted by b, by substituting the given point (5,2) into our line from above, that is,
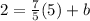
which gives
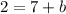
then, by subtracting 7 to both sides, we get

or equivalently,
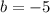
Finally, by substituting this value into our line model, the answer is: