Question

Coulomb's law for the magnitude of the force F between two particles with charges Q and Q′ separated by a distance d is|F|=K|QQ′|d2,where K=14πϵ0, and ϵ0=8.854×10−12C2/(N⋅m2) is the permittivity of free space.Consider two point charges located on the x axis: one charge, q1 = -16.5 nC , is located at x1 = -1.710 m ; the second charge, q2 = 36.0 nC , is at the origin (x = 0).What is (Fnet3)x , the x-component of the net force exerted by these two charges on a third charge q3 = 52.5 nC placed between q1 and q2 at x3 = -1.115 m ?Your answer may be positive or negative, depending on the direction of the force.

Answer 1

Given:

The charge

`\begin{gathered} q1=\text{ -16.5 nC} \\ =-16.5\text{ }*10^(-9)\text{ C} \end{gathered}`

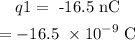
The charge q1 is located at

`x1\text{ = -1.71 m}`

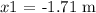
The charge

`\begin{gathered} q2\text{ = 36 nC} \\ =\text{ 36 }*10^(-9)\text{ C} \end{gathered}`

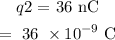
The charge q2 is located at x2 = 0

The charge

`\begin{gathered} q3\text{ = 52.5 nC} \\ =52.5\text{ }*10^{-9\text{ }}C \end{gathered}`

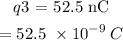
The charge q3 is located at

`x3\text{ = -1.115 m}`

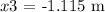
To find the net force on charge q3.

Step-by-step explanation:

The force on charge q3 due to q1 is

`\begin{gathered} F_(13)=\text{ K}(|q1q3|)/((x1-x3)^2) \\ =9*10^9*(|(-16.5)*10^(-9)*52.5*10^9|)/((-1.71+1.115)^2) \\ =2.2*10^(-5)\text{ N} \end{gathered}`

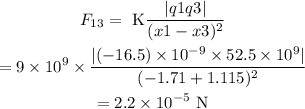
The force on the charge q3 due to q2 is

`\begin{gathered} F_(23)=K(|q2q3|)/((x2-x3)^2) \\ =9*10^9*(|36*10^(-9)*52.5*10^(-9)|)/((0+1.115)^2) \\ =1.368\text{ }*10^(-5)\text{ N} \end{gathered}`

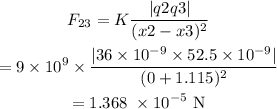
The forces acting on q3 can be represented as

Thus, the net force will be

`\begin{gathered} F_(net)=\text{ F}_(13)+F_(23) \\ =2.2*10^(-5)+1.368*10^(-5) \\ =3.568*10^(-5)\text{ N} \end{gathered}`

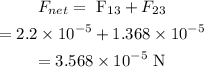
The direction of the force will be negative as it lies on the negative x-axis.