We have a rectangular room with the following dimensions:
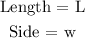
The dimensions of the rectangular room is related to each other by the following statement:
" 3 meters longer than it is wide "
We will go ahead an decrypt the above statement and express it into a mathematical form in terms of the dimensions ( defined above ) of the rectangular room:

The next statement relates the perimeter ( P ) of the rectangular room in terms of its previously defined dimensions.
" perimeter is 30 meters "
We will go ahead an decrypt the above statement and express it into a mathematical form in terms of the dimensions ( defined above ) of the rectangular room:
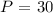
The perimeter of a rectangle ( P ) is defined as the sum of all the boundary sides which can be expressed in terms of its length ( L ) and width ( w ) as follows:
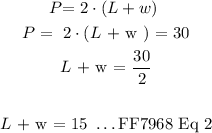
Now we have two equations ( Eq1 and Eq2 ) which are just mathematical decryption of the statements provided in the question and these equations are expressed in terms of two variables ( L and w ).
We have two equations and two unknowns we can solve these equations simultaneously.
Step 1: Substitute Eq1 into Eq2.

Step 2: Solve the Eq3 for the variable ( w ).

Step 3: Back-substitution of the result of one variable ( w ) into Eq1.
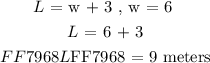
The solution to the two equations are given as:
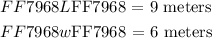
Answer:
Length ( L ) = 9 meters , Width ( w ) = 6 meters