From the dot plot, we have the following data:
For 6th grade:
Number of students Frequency(hours)
1 2
4 3
2 4
4 5
5 6
1 7
1 9
2 10
Now let's write down the number of hours, arranging them in ascending order:
2, 3, 3, 3, 3, 4, 4, 5, 5, 5, 5, 6,6,6,6,6,7,9,10,10
To find the median of 6th grade, we sum up the two middle numbers, which are 5 and 5, and divide by 2.
Thus:
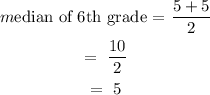
Median of hours that 6th grade play sports = 5 hours
Lets also use the same method to find the median for 8th grade.
For 8th grade:
Number of students Frequency(hours)
1 2
1 3
2 4
2 6
4 7
5 8
2 9
3 10
Now let's write down the number of hours, arranging them in ascending order:
2,3,4,4,6,6,7,7,7,7,8,8,8,8,8,9,9,10,10,10
To find the median of 8th grade, we sum up the two middle numbers, which are 7 and 7, and divide by 2.
Thus:
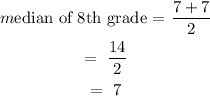
Median of hours that 8th graders play sports = 7 hours
The difference between the median number of hours that sixth graders play sports and the median number of hours that 8th graders play sports will be:
![\begin{gathered} (\operatorname{median}\text{ of hours 8th graders play) - ( median of hours 6th graders play)} \\ =\text{ 7 - 5} \\ =\text{ 2 hours} \end{gathered}]()
ANSWER:
2 HOURS