We are given the following sequence:
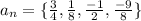
We notice that each term is determined by adding -5/8 to the previous term, like this:
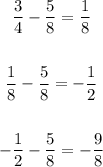
Therefore, the sequence is an arithmetic sequence with a common difference of -5/8.
Arithmetic sequences are convergent only when the common diference is zero, therfore, the sequence is divergent.