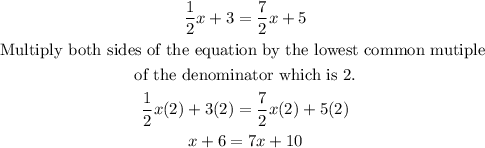Question

Please help! This assignment is due soon! (In The photo)

Answer 1

Elena must have substracted 1/2x from both sides of the equation.

Lin must have multiplied both sides of the equation by 2

Step-by-step explanation

The equation given is

`(1)/(2)x+3=(7)/(2)x+5`

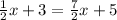
For Elena to have arrived at

`3=(7)/(2)x-(1)/(2)x+5`

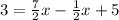
Then Elena must have substracted 1/2x from both sides of the equation.

That is;

`\begin{gathered} (1)/(2)x+3=(7)/(2)x+5 \\ \text{Substracting }(1)/(2)x\text{ from both sides of the equation will give Elena first step} \\ (1)/(2)x+3-(1)/(2)x=(7)/(2)x+5-(1)/(2)x \\ 3=(7)/(2)x-(1)/(2)x+5 \end{gathered}`

For Lin to have arrived at

`x+6=7x+10`

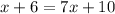
It shows Lin must have multiplied both sides of the equation by 2

That is;

`\begin{gathered} (1)/(2)x+3=(7)/(2)x+5 \\ \text{Multiply both sides of the equation by the lowest common mutiple } \\ \text{of the denominator which is 2.} \\ (1)/(2)x(2)+3(2)=(7)/(2)x(2)+5(2) \\ x+6=7x+10 \end{gathered}`