We are asked to find the left and right hand limits of the given function.
1. Left-hand limit:
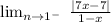
The numerator is negative when we substitute -1, so the absolute value will be evaluated as a negative expression.
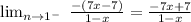
Now, factor the numerator
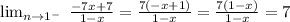
So, the left-hand limit is equal to 7
2. Right-hand limit:
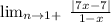
The numerator is positive when we substitute +1, so the absolute value will be evaluated as a positive expression.
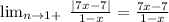
Now, factor the numerator and the denominator.
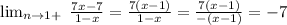
So, the right-hand limit is equal to -7