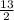Given the equation:

Where r and s are two solutions of the equation and r is greater than x.
Let's solve for r - s.
To find the solutions, let's use the quadratic formula:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Where:
a = 2
b = 7
c = -15
Thus, we have:
![\begin{gathered} x=\frac{-7\pm\sqrt[]{7^2-4(2)(-15)}}{2(2)} \\ \\ x=\frac{-7\pm\sqrt[]{49+120}}{4} \\ \\ x=\frac{-7\pm\sqrt[]{169}}{4} \\ \\ x=(-7\pm13)/(4) \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/m0z3tgm0nwvmvrbx173chboskgnv08izen.png)
Solving further:
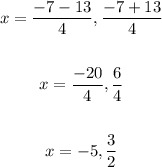
The solutions to the equation are: -5 and 3/2
SInce r is greater than s, we have:
r = 3/2
s = -5
Hence, to find r - s, let's subtract -5 from 3/2:
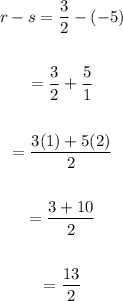
Therefore, the value of r - s is:
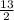
ANSWER: B