Question

The weight of passengers on a roller coaster increases by 50%as the car goes through a dip with a 30 m radius of curvature.What is the car’s speed at the bottom of the dip?

Answer 1

12.12 m/s

Step-by-step explanation:

The net force of the car at the bottom of the dip is equal to

`\begin{gathered} F__(net)=F_(seat)-mg=ma_c \\ F_n-mg=m(v^2)/(r) \end{gathered}`

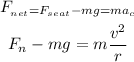
Where Fn is the normal force that acts upwards, m is the mass of the car, g is the gravity, v is the car's speed at the bottom of the dip and r is the radius.

We know that the weight of the passenger increase by 50%, so

Fn = 1.5mg

Replacing this on the first equation and solving for the car speed v, we get

`\begin{gathered} 1.5mg-mg=(mv^2)/(r) \\ 0.5mg=(mv^2)/(r) \\ 0.5g=(v^2)/(r) \\ 0.5gr=v^2 \\ v=√(0.5gr) \end{gathered}`

Finally, replacing g = 9.8 m/s² and r = 30 m, we get:

`v=√(0.5(9.8)(30))=12.12\text{ m/s}`

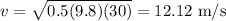
So, the car’s speed at the bottom of the dip is 12.12 m/s