Question

F(x)=-2(x-1)^2+2 a) standard form b) graph

Answer 1

a) f(x) = -2x² + 4x

Step-by-step explanation:

To find the standard form we need to solve the equation as:

`\begin{gathered} f(x)=-2(x-1)^2+2 \\ f(x)=-2(x^2-2x+1)+2 \\ f(x)=-2x^2-2(-2x)-2(1)+2 \\ f(x)=-2x^2+4x-2+2 \\ f(x)=-2x^2+4x \end{gathered}`

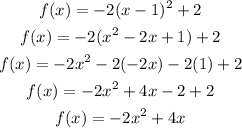
So, the standard form is f(x) = -2x² + 4x

To make the graph we will use the initial form because when the equation is written like f(x) = a(x-h)²+k, the coordinate (h,k) is the vertex of the parabola

So, in this case, the vertex of the parabola is the point (1, 2)

On the other hand, we can find a point in the graph. For example, if x is equal to 0, then f(x) is equal to:

f(x) = -2(x-1)² + 2

f(0) = -2(0-1)² + 2

f(0) = -2(-1)² + 2

f(0) = - 2 + 2

f(0) = 0

So, the parabola passes through the point (0,0) and has a vertex in the point (1, 2). Then, the graph is: