Question

6. The table below shows the population of Florida from 2010 to 2019. Year Population (millions) 2010 18.7 2011 19.1 2012 19.3 2013 19.6 2014 19.9 2015 20.2 2016 20.6 2017 21.0 2018 21.2 2019 21.5 (a) Use a graphing calculator to build a logistic regression model that best fits this data, letting t = 0 in 2010. Round each coefficient to two decimal places. P t = (b) What does this model predict that the population of Florida will be in 2030? Round your answer to one decimal place. million people (c) When does this model predict that Florida's population will reach 23 million? Give your answer as a calendar year (ex: 2010). During the year (d) According to this model, what is the carrying capacity for Florida's population? million people

Answer 1

Step 1:

In this question, we are given the following:

Step 2:

a) Using a graphing calculator to build a logistic regression model that fits the data, letting t=0. We are to round each coefficient to two decimal places:

From the graph, the logistic regression model ( to 2 decimal places) is given as:

`P_t\approx\text{ }(37.39)/(1+e^(-0.03t))`

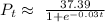
b ) What does this model predict that the population of Florida will be in 2030? We are to round the answer to one decimal place.

If 2010 represents t= 0,

Then 2030 will be t = 20,

Then, we put t=20 into the logistic regression model, then we have that:

From the graph, we can see that:

From the graph, we see that the model predicted that the population of Florida will be approximately 25 million people ( to one decimal place).

c) When does this model predict that Florida's population will reach 23 million? Give your answer as a calendar year (ex: 2010).

From the graph, we can see clearly that the model predicted that Florida's population will reach 23 million in approximately 14 years which is in the Year 2024.

d) According to this model, what is the carrying capacity for Florida's population?

`\begin{gathered} \text{Given that:} \\ P(t)_{}\approx\text{ }(37.39)/(1+e^(-0.03t)) \\ \text{When t is too large, t=}\infty\text{ , we have that:} \\ P(\infty\text{ ) = }(37.39)/(1+e^(-\infty)) \\ P(\infty)\text{ = }(37.39)/(1+0)\text{ } \\ P(\infty\text{ ) = }(37.39)/(1)\text{ = 37.39 } \end{gathered}`

From the calculation, we can see clearly that the carrying capacity for Florida's population is approximately 37.39 million people.