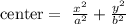Question

les pes and down and the the venue toci endpoints of the teamcarcade and When draw the hyperbola tor each equation problem (h) - 416 as 35

Answer 1

EXPLANATION

Given the equation

(b)

`9x^2-y^2=9`

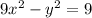
First, we need to find the vertex applying the following formula:

The vertices (h+a, k), (h-a,k) are the two bending points of the hyperbola with center (h,k) and semi-axis (a,b)

Calculate hyperbola properties:

Hyperbola standard equation:

`((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1`

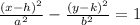
Rewrite 9x^2 -y^2 = 9 in the form of a standard hyperbola equation:

Divide by coefficient of square terms: 9

`x^2-(16)/(9)y^2=16`

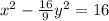
Divide by coefficient of square terms: 16

`(1)/(16)x^2-(1)/(9)y^2=1`

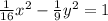
Refine:

`(x^2)/(16)-(y^2)/(9)=1`

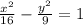
Rewrite in standard form:

`((x-0)^2)/(4^2)-((y-0)^2)/(3^2)=1`

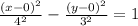
Therefore, hyperbola properties are:

(h,k) = (0,0) , a=4, b=3

Refine:

(4,0), (-4,0)

Now we need to compute the foci:

For a right-left faccing hyperbola, the foci are defined as (h+c,k), (h-c,k), where c= sqrt(a^2+b^2) is the distance from the center (h,k) to a focus.

Computing c (we have previously calculated a=4 and b=3):

`c=\sqrt[]{4^2+3^2}=\sqrt[]{16+9}=\sqrt[]{25}=5`

Refine:

Foci: (5,0), (-5,0)

Next, we need to find the asymptotes:

The asymptotes are the lines the hyperbola tends to at +- infinite

For right-left hyperbolas the asymptotes are:

`y=\pm(b)/(a)(x-h)`

Substituting terms:

`y=\pm(3)/(4)(x-0)+0`

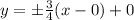
Refine:

`y=(3x)/(4),\text{ y=-}(3x)/(4)`

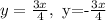
Now, we need to find the vertices:

The endpoints are:

(4,0) , (-4,0)

Now, we need to find the center:

`\text{center}=\text{ }(x^2)/(a^2)+(y^2)/(b^2)`