Question

You pick up a 7kg bag and lift to a height of 0.7m. You proceed to walk down the hallway 25m carrying the bag. You stop and lift the bag from 0.7m to a height of 0.95m. You continue to walk another 10m and then stop for 75s to talk to your friend. How much work did you perform on the bag throughout the whole scenario ? If it took you 0.95s to lift the bag to a height of 0.7m, how much power did you generate ?

Answer 1

Work done in the whole motion

We know that the work done againts gravity is related to the potential energy as:

`W=\Delta U`

where:

`U=mgh`

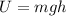
is the potential energy of the object.

We also know that the work is related to the kinetic energy by:

`W=\Delta K`

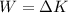
where:

`K=(1)/(2)mv^2`

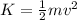
is the kinetic energy.

Now that we remembered this we have to break down the motion into parts, let's do this:

0. You pick up the bag to the 0.7 m height.

,

1. You walk 25 meters down the hall.

,

2. You lift the bag from 0.7 m to 0.95 m.

,

3. You walk 10 m.

To find the total work you performed we will analyze we will find the work done in each part and then we will add them.

Fist part of the motion.

In this case the initial height is zero and the final height is 0.7 m then we have:

`\begin{gathered} W_1=(7)(9.8)(0.7)-(7)(9.8)(0) \\ W=48.02 \end{gathered}`

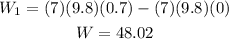
Hence in this part you perfomed 48.02 J of work.

Second part of the motion.

Since you, at first, were at rest this means that your initial velocity for this part of the motion is zero. Then you walked down the hall 25 m and then you stopped again and hence your final velocity was zero as well. This means that the change in kinetic energy is:

`\begin{gathered} W_2=(1)/(2)(7)(0)^2-(1)/(2)(7)(0)^2 \\ W_2=0 \end{gathered}`

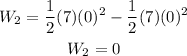
Hence in this part of the motion you performed 0 J of work (this means that in this part you performed no work).

Third part of the motion.

In this case the initial height is 0.7 m and the final height is 0.95 m, then we have:

`\begin{gathered} W_3=(7)(9.8)(0.95)-(7)(9.8)(0.7) \\ W_3=17.15 \end{gathered}`

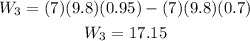
Therefore in this part you performed 17.15 J of work.

Fourth part of the motion.

Similarly to part two of the motion in this case you both began and finish at rest, hence the change in velocity is zero and the work done is zero.

Total work done.

Once we know the work done in each part of the motion we add them to find the total work done, then we have:

`\begin{gathered} W=48.02+0+17.15+0 \\ W=65.17 \end{gathered}`

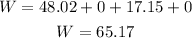
Therefore, the work you perfomed in the whole scenario was 65.17 J

Power generated in the first part of the motion.

The power is given by:

`P=(W)/(t)`

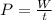
We know that when you lifted the bag to a hight of 0.7 m you performed 48.02 J, if this took 0.95 s then the power is:

`\begin{gathered} P=(48.02)/(0.95) \\ P=50.54 \end{gathered}`

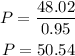
Therefore you perfomed 50.54 W of power (This can be rounded down to 50W)