Question

you roll a six-sided die find the probability of the following scenario A.rolling a 6 or a number greater than. threeB rollicking a number less than 5 or an even number c rolling a 2 or an odd number

Answer 1

We have a six-sided die and we have to calculate the probability of different scenarios.

We know that each number, from 1 to 6, has a probability of 1/6.

A) We have to calculate the probability of rolling a 6 or a number greater than 3.

As rolling a 6 is also rolling a number greater than 3, its probability is included in the event of rolling a number greater than 3.

We can write the probability of this event as:

`P(x>3)=P(x=4)+P(x=5)+P(x=6)`

This means that the probability of rolling a number greater than 3 is equal to the probability of getting a 4, a 5 or a 6.

Then, replacing by the proability values, we get:

`P(x>3)=P(x=4)+P(x=5)+P(x=6)=(1)/(6)+(1)/(6)+(1)/(6)=(3)/(6)=(1)/(2)`

The probability for this scenario is P(x>3) = 1/2.

B) We have to calculate the probability of rolling a number less than 5 or an even number.

In this case, the only event that is not included is rolling a 5, as 5 is not less than 5 and it is also not an even number. Then, we can write this probability as 1 less the probability of rolling a 5:

`P(x<5\text{ or }x\colon even)=P(x<5)+P(x=6)=1-P(x=5)=1-(1)/(6)=(5)/(6)`

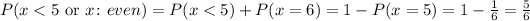
Then, the probability of this event is P(x≠5) = 5/6.

C) In this case, the event is rolling a 2 or an odd number (1, 3 or 5).

Then, in this case, the probability can be written as:

`\begin{gathered} P(x=2\text{ or }x\colon odd)=P(x=2)+P(x=1)+P(x=3)+P(x=5) \\ P(x=2\text{ or }x\colon odd)=(1)/(6)+(1)/(6)+(1)/(6)+(1)/(6)=(4)/(6)=(2)/(3) \end{gathered}`

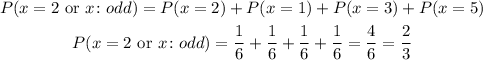
For this event, the probability is P = 2/3.

Answer:

A) 1/2

B) 5/6

C) 2/3

NOTE: If we have to express the probabilities in decimals, we will get:

A) 1/2 = 0.5

B) 5/6 = 0.833

C) 2/3 = 0.667