To determine the area of the shaded sector, we use the formula below.
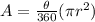
Based on the question, the given information are:
• radius = 16 meters
,
• central angle = 62°
,
• pi value = 3.14159
Let's plug the given information into the formula above.
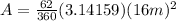
Then, solve.
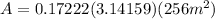
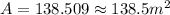
Therefore, the area of the shaded sector is approximately 138.5m². (Option C)