Question

Match each equation on the left with its equivalent logarithmic form. (2 points) NER 2 (e3t) 12 1 1 12 (e3t) = 2 111 HR JE M 1 HUN 3 (ezt) = 12 :: 3t = log 6 :: 2t = log, 4 loge

Answer 1

Let's solve each equation to find the right match.

`2(e^(3t))=12`

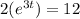
First, we divide the equation by 2.

`\begin{gathered} (2(e^(3t)))/(2)=(12)/(2) \\ e^(3t)=6 \end{gathered}`

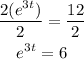
Then, we apply logarithms on each side.

`\begin{gathered} \log _e(e^(3t))=\log _e(6) \\ 3t=\log _e(6) \end{gathered}`

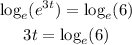
So the first expression matches the first answer choice.

The second equation is

`12(e^(3t))=2`

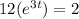
First, we divide the equation by 12.

`\begin{gathered} (12(e^(3t)))/(12)=(2)/(12) \\ e^(3t)=(1)/(6) \end{gathered}`

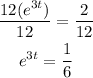
Then, we apply logarithms on each side.