We have a sequence where we know that the initial term a0 is 25.
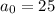
Then, each term adds the common difference of 15, so we can write:
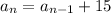
The recursive formula for this sequence, representing how much she has in her savings account, is a(n) = a(n-1) + 15.
To find the explicit formula, we relate each term to the first term in order to find the relation:

Then, the explicit formula is a(n) = 25 + 15n.
Answer:
Recursive formula: a(n) = a(n-1) + 15
Explicit formula: a(n) = 25 + 15n