Question

Hello i need help please. Also, how much money was invested at 5% loss??

Answer 1

Let the amount partially invested out of $21,020 be x for 12% annual interest;

So, the interest gotten from this investment is;

`\begin{gathered} I=(12x)/(100) \\ \text{But A=P+I} \\ \text{Where P is the amount invested, A is the amount and I is the interest} \end{gathered}`

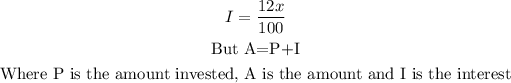
Thus the amount from this investment is;

`\begin{gathered} A=(12x)/(100)+x \\ A=1.12x \end{gathered}`

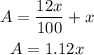
Thus, the rest of the money after x has been invested is;

`21020-x`

And since this money suffered a loss of 5%, we have the amount from this investment as;

`\begin{gathered} A=(21020-x)-((5)/(100)(21020-x)) \\ A=21020-x-1051+0.05x \\ A=19969-0.95x \end{gathered}`

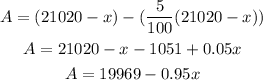
Thus, the total income from both investments is $2026.

Then, the total amount after both investments is;

`21020+2026=23046`

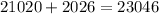
Then, we can get the money invested x at 12% annual interest as;

`\begin{gathered} 23046=1.12x+19969-0.95x \\ 23046-19969=1.12x-0.95x \\ 0.17x=3077 \\ x=(3077)/(0.17) \\ x=18100 \end{gathered}`

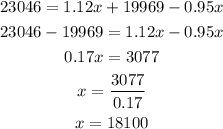
The money invested at 12% annually is $18100.

The amount invested at 5% loss is;

`21020-18100=2920`

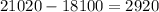
The amount invested at 5% loss is $2920