Question

No need to give a whole explanation, I just need the answer because I'm in a rush. Thank you

Answer 1

We have to locate each approximation of pi in the ruler.

3.14 correspond to 3.14, the leftmost blank space.

22/7 is approximately 3.1428, so it should be located at the rightmost blank.

In the middle we can place pi, that is approximately 3.1415.

We can calculate which of the approximations is better by calculating the difference between the approximation and the "real" value (it is always an approximation) of pi.

For 3.14, we will have a difference of:

`\pi-3.14\approx3.14159-3.14=0.00159`

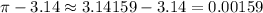
For 22/7 we will have a difference of:

`\pi-(22)/(7)\approx3.14159-3.14286=-0.00127`

The absolute value of the difference is smaller for 22/7, so 22/7 is a closer approximation than 3.14.

If we have a number x so that x/113 has to be a better approximation to pi than 22/7, we should write:

`\begin{gathered} (x)/(113)=\pi \\ x=113\cdot\pi \\ x\approx355 \end{gathered}`

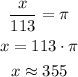
If we calculate 355/113 and compare it to pi we would get a difference of:

`\pi-(355)/(113)\approx3.1415926-3.1415929=-0.0000003`

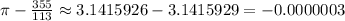
Answer: the blanks should be filled from left to right with 3.14, pi and 22/7.

The closer approximation is 22/7.

For x/113, the value of x to be a better approximation to pi than 22/7 should be x=355.