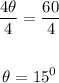How do I solve this problem? Solve the following trig functions and express your solution in degrees.

Question

asked Mar 7, 2023 14.7k views

1 Answer

Geet Thakur · Answer 1 · 2023-03-14T04:56:00+0000

Given the equation:

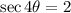
$\sec 4\theta=2$

Let's solve the trigonometric function and express the solution in degrees.

The first step is to take the inverse secant of both sides:

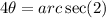
$\begin{gathered} 4\theta=arc\sec (2) \\ \end{gathered}$

Where:

Exact value of arcsec(2) = 60

Hence, we have:

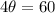
$4\theta=60$

The next step is to divide both sides by 4:

$\begin{gathered} (4\theta)/(4)=(60)/(4) \\ \\ \theta=15^0 \end{gathered}$