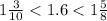Answer:
Step-by-step explanation:
Given the below numbers;
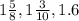
To be able to order the above numbers from the least to the greatest, let's first convert the mixed numbers to improper fractions as seen below;
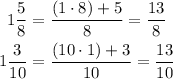
Let's now convert the improper fractions to decimal numbers;
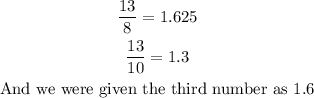
From the above, we can go and order the numbers from the least to greatest as;