Step-by-step explanation
The given question can be solved if we simplify the given expression
We are given the expression:
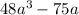
To find the equivalent expression, we can factorize
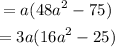
Thus, we have 3a(16a²-25)
We can simplify further by applying the difference of two squares
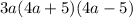
Hence, we also have 3a(4a+5)(4a-5)
Also, we can re-write the expression as
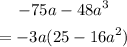
Thus, we will have
-3a(25-16a²)
Therefore, we have 3 answers
3a(16a²-25)
3a(4a+5)(4a-5)
-3a(25-16a²)