Question

A ball is thrown from a height of 182 feet with anh=182-121-167How long after the ball is thrown does it hit theRound your answer(s) to the nearest hundredt(If there is more than one answer, use the 'or

Answer 1

The height of the ball (in feet) after t seconds is given by the equation:

`h(t)=182-12t-16t^2`

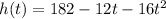
Note that for t = 0 the height is 182 feet, the initial height. It's required to find the value of t at the moment when the ball hits the ground, that is, when h = 0:

`182-12t-16t^2=0`

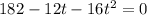
Rearranging:

`-16t^2-12t+182=0`

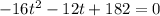
This is a quadratic equation with coefficients:

a = -16, b = -12, c = 182.

We need to apply the quadratic formula:

`t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Substituting:

`t=(-(-12)\pm√((-12)^2-4(-16)(182)))/(2(-16))`

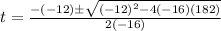
Operating:

`t=(12\pm√(144+11648))/(-32)`

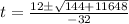
Calculating:

`t=(12\pm108.591)/(-32)`

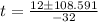
There is one positive solution and one negative solution. We only take the positive solution because the time cannot be negative in this context.

The positive solution is:

`t=(12-108.591)/(-32)`

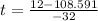
Calculating: t = 3.018 seconds.

Rounding to the nearest hundredth: t = 3.02 seconds