Question

Please help me ASAP!!

Answer 1

We can find this point as the intersection point between the two profits functions:

`\begin{gathered} P_1(x)=P_2(x) \\ -0.05x^2+20x-500=-0.1x^2+30x-500 \\ -0.05x^2+0.1x^2+20x-30x-500+500=0 \\ 0.05x^2-10x=0 \\ 0.05x(x-200)=0 \\ x_1=0 \\ x_2=200 \end{gathered}`

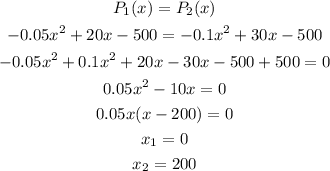
From this expression we know that the companies made the same profit when they made no units (x=0) or they made 200 units (x=200). We will ignore x=0 as a solution because it is trivial.

Then, the profit for 200 units can be calculated with any of the two profit functions, as they have the same value for x=200:

`\begin{gathered} P(200)=-0.05\cdot200^2+20\cdot200-500 \\ P(200)=-0.05\cdot40000+4000-500 \\ P(200)=-2000+4000-500 \\ P(200)=1500 \end{gathered}`

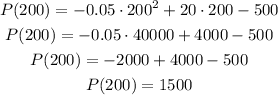
Answer: both factories will have the same profit when they manufacture 200 chairs because each factory earns a profit of $1500 {fourth option].