Question

Need help with both c and e for this question. It is for homework. Please let me know if you cannot do both!!

Answer 1

Step-by-step explanation

When you ask a student of the sample if he/she knows the channel there are only two possible outcomes: yes or no. This means that we are dealing with a binomial probability distribution problem. Asking a student if he/she knows the channel is considered a "trial", the number of students in the sample is the number of trials that we'll name n, an student answering that he/she knows the channel will be considered a "success" and the number of successes in the sample (i.e. the number of students from the sample knowing the channel) will be k. We know that the probability that a student knows the channel is 0.6 (this is 60% written as a fraction), this is the probability of success in a single trial and we are going to use p to refer to it.

For a binomial probability distribution the probability of having k successes in n trials with a single trial probability p is given by the following formula:

`P(k,n)=(n!)/((n-k)!k!)\cdot p^k\cdot(1-p)^(n-k)`

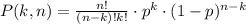
The probability that at most 3 student out of the total 15 students in the sample know the channel is given by the sum of 4 probabilities:

- The probability that no student knows the channel P(0,15).

- The probability that 1 student knows the channel P(1,15).

- The probability that 2 students know the channel P(2,15).

- The probability that 3 students know the channel P(3,15).

So we have to find each of these probabilities and then we add them. We begin with P(0,15):

`P(0,15)=(15!)/((15-0)!0!)0.6^0(1-0.6)^(15-0)=1\cdot1\cdot0.4^(15)=0.000001`

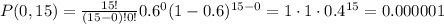
Then P(1,15):

`P(1,15)=(15!)/((15-1)!1!)0.6^1(1-0.6)^(15-1)=15\cdot0.6\cdot0.4^(14)=0.00002`

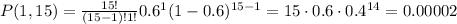
And P(2,15):

`P(2,15)=(15!)/((15-2)!2!)0.6^2(1-0.6)^(15-2)=105\cdot0.6^2\cdot0.4^(13)=0.00025`

And P(3,15):

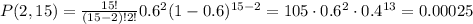
`P(3,15)=(15!)/((15-3)!3!)0.6^3(1-0.6)^(15-3)=455\cdot0.6^3\cdot0.4^(12)=0.00165`

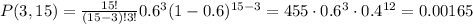
Then we add the four probabilities:

`\begin{gathered} P(0,15)+P(1,15)+P(2,15)+P(3,15)=0.000001+0.00002+0.00025+0.00165 \\ \begin{equation*} 0.000001+0.00002+0.00025+0.00165=0.001921 \end{equation*} \end{gathered}`

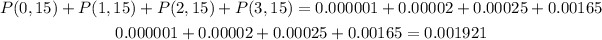
So the probability is 0.001921.

In part e we must find the probability that less than 3 know the channel. This is given by the sum of P(0,15), P(1,15) and P(2,15) so we get:

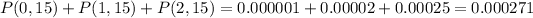
`P(0,15)+P(1,15)+P(2,15)=0.000001+0.00002+0.00025=0.000271`Answer

We must round the answers to 4 decimal places so the answers are:

c. 0.0019

e. 0.0003