Question

Given the dimensions of the frustum, find the volume in terms of pi.

Answer 1

We are asked to find the volume of the given frustum.

Recall that the volume of a frustum is given by

`V=(1)/(3)\cdot h\cdot(B_1+B_2+\sqrt[]{B_1B_2})`

Where h is the height, B₁ is the lower area and B₂ is the upper base area of the frustum.

The lower base area (B₁) is given by

`B_1=\pi r^2_1=\pi(21)^2=441\pi\: in^2`

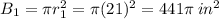
The upper base area (B₂) is given by

`B_2=\pi r^2_2=\pi(7)^2=49\pi\: in^2`

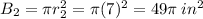
Finally, substitute all the values into the above volume formula

`\begin{gathered} V=(1)/(3)\cdot h\cdot(B_1+B_2+\sqrt[]{B_1B_2}) \\ V=(1)/(3)\cdot24\cdot(441\pi+49\pi_{}+\sqrt[]{441\pi\cdot49\pi}) \\ V=(1)/(3)\cdot24\cdot(441\pi+49\pi_{}+147\pi) \\ V=(1)/(3)\cdot24\cdot(637\pi) \\ V=(1)/(3)\cdot15288\pi \\ V=5096\pi\: in^3 \end{gathered}`

Therefore, the volume of the frustum is 5096π cubic inches.